Question

An employer interviews 10 people for 6 technical support positions in a company, and 5 of the 10 people are women. If all 10 are qualified, in how many ways can the employer fill the technical support positions if exactly 3 are women?

Answer 1

Let the people be {M1, M2, M3, M4, M5, W1, W2, W3, W4, W5}

where M1 is Man 1, W1 woman 1 and so on...


The formula
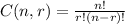
`C(n, r)= (n!)/(r!(n-r)!)`, gives the total numbers of ways of creating groups of r out of n.

r! means 1*2*3*...(r-1)*r.


The technical support group is going to have exactly 3 women, which will be chosen from 5 women, and 3 men which will be chosen from 5 men.

Each of the selections can be done in C(5, 3) many ways, and since the any selection of the men and women can be combined, in total there are:

C(5,3) *C(5, 3) many ways of creating the technical support group.


`C(5,3) = (5!)/(3!2!)= (5*4*3*2*1)/(3*2*1*2*1)=10`

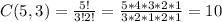
10*10=100 many ways of forming the group.


Answer: 100