Answer:
We have function,
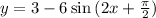
Standard Form of Sinusoid is
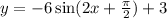
Which corresponds to
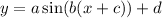
where a is the amplitude
2pi/b is the period
c is phase shift
d is vertical shift or midline.
In the equation equation, we must factor out 2 so we get
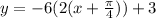
Also remeber a and b is always positive
So now let answer the questions.
a. The period is
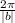
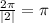
So the period is pi radians.
b. Amplitude is
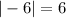
Amplitude is 6.
c. Domain of a sinusoid is all reals. Here that stays the same. Range of a sinusoid is [-a+c, a-c]. Put the least number first, and the greatest next.
So using that rule, our range is [6+3, -6+3]= [9,-3] So our range is [-3,9].
D. Plug in 0 for x.
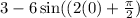
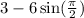
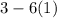
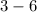

So the y intercept is (0,-3)
E. To find phase shift, set x-c=0 to solve for phase shift.
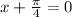
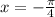
Negative means to the left, so the phase shift is pi/4 units to the left.
f. Period is PI, so use interval [0,2pi].
Look at the graph above,