Question

100 points!!! Pre calculus. I need helpppppppppp

Answer 1

We have function,

`y = 3 - 6 \sin {}^{} (2x + (\pi)/(2) )`

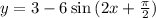
Standard Form of Sinusoid is

`y = - 6 \sin(2x + (\pi)/(2) ) + 3`

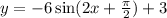
Which corresponds to

`y = a \sin(b(x + c)) + d`

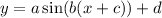
where a is the amplitude

2pi/b is the period

c is phase shift

d is vertical shift or midline.

In the equation equation, we must factor out 2 so we get

`y = - 6(2(x + (\pi)/(4) )) + 3`

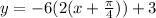
Also remeber a and b is always positive

So now let answer the questions.

a. The period is

`(2\pi)/( |b| )`

`(2\pi)/( |2| ) = \pi`

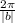
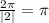
So the period is pi radians.

b. Amplitude is

`| - 6| = 6`

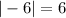
Amplitude is 6.

c. Domain of a sinusoid is all reals. Here that stays the same. Range of a sinusoid is [-a+c, a-c]. Put the least number first, and the greatest next.

So using that rule, our range is [6+3, -6+3]= [9,-3] So our range is [-3,9].

D. Plug in 0 for x.

`3 - 6 \sin((2(0) + (\pi)/(2) )`

`3 - 6 \sin( (\pi)/(2) )`

`3 - 6(1)`

`3 - 6`

`= - 3`

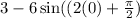
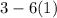
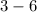
So the y intercept is (0,-3)

E. To find phase shift, set x-c=0 to solve for phase shift.

`x + (\pi)/(4) = 0`

`x = - (\pi)/(4)`

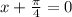
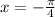
Negative means to the left, so the phase shift is pi/4 units to the left.

f. Period is PI, so use interval [0,2pi].

Look at the graph above,

Answer 2

a. π

b. 3

c. Domain = (-∞, ∞)

Range = [-3, 9]

d. (0, 3)

e. π/4

f. See attachment 1.

Explanation:

Standard form of a sine function

`\text{f}(x)=\text{A} \sin \left(\text{B}\left(x+\text{C}\right)\right)+\text{D}`

where:

• |A| = Amplitude (height from the mid-line to the peak).
• 2π/B = Period (horizontal distance between consecutive peaks).
• C = Phase shift (horizontal shift - positive is to the left).
• D = Vertical shift (y=D is the mid-line of the function).

Given function:

`y=3-6 \sin \left(2x+(\pi)/(2)\right)`

Rearrange to standard form:

`y=-6 \sin \left(2\left(x+(\pi)/(4)\right)\right)+3`

Therefore:

• |A| = 6
• B = 2
• C = π/4
• D = 3

Part (a)

`\sf Period & = (2 \pi)/(B)= (2 \pi)/(2)=\pi`

Part (b)

Amplitude = 6

Part (c)

The domain of a function is the set of all possible x-values.

As a sine function is continuous, the domain is unrestricted: (-∞, ∞).

The range of a function is the set of all possible y-values.

As the vertical shift of the function is 3, the mid-line of the function is y=3.

As the amplitude is 6, the range is restricted to 6 more or 6 less than the mid-line: [-3, 9].

Part (d)

The y-intercept of the graph is when x = 0.

Substitute x = 0 into the function and solve for y:

`\implies y=3-6 \sin \left(2(0)+(\pi)/(2)\right)`

`\implies y=3-6 \sin \left((\pi)/(2)\right)`

`\implies y=3-6 \sin \left(1\right)`

`\implies y=3-6`

`\implies y=-3`

Part (e)

`\sf Phase \; shift=(\pi)/(4)\;(to\;the\;left)`

Part (f)

The x-intercepts of the graph are when y = 0.

Substitute y = 0 into the function and solve for x:

`\implies 3-6 \sin \left(2x+(\pi)/(2)\right)=0`

`\implies -6 \sin \left(2x+(\pi)/(2)\right)=-3`

`\implies \sin \left(2x+(\pi)/(2)\right)=(1)/(2)`

`\implies 2x+(\pi)/(2)=\sin^(-1) \left((1)/(2)\right)`

`\implies 2x+(\pi)/(2)=(\pi)/(6)+2\pi n, \;\;(5\pi)/(6)+2\pi n`

`\implies 2x=-(\pi)/(3)+2\pi n, \;\;(\pi)/(3)+2\pi n`

`\implies x=-(\pi)/(6)+\pi n, \;\;(\pi)/(6)+\pi n`

See attachment 1 for the sketch of the graph.