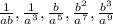Question

The first term of a geometric series is a/b^2, and the common ratio is b/a^2. Find the next five terms of the geometric sequence.

Answer 1

Here it is in order (2nd to 6th):
1/ab, 1/a^3, b/a^5, b^2/a^7, b^3/a^9

Hope this helps!

Answer 2

the next five terms are:

`(1)/(ab) , (1)/(a^(3) ) ,(b)/(a^(5) ) ,(b^(2) )/(a^(7) ) ,(b^(3) )/(a^(9) )`

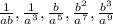
Explanation:

A geometric serie is a succession of terms on which every terms is the result of the last term multiply to a common ratio. for example, a geometric serie with inicial terms equal to 2 and the common ratio is 3, the four first numbers of the serie is given by

2, 6, 18, 54

Where every term is calculate as:

first term = 2

second term = first term x common ratio = 2 * 3 = 6

third term = second term x common ratio = 6 * 3 = 18

fourth term = third term x common ratio= 8 * 3 = 54

Then, with this exercise we have the same situation, the first term is
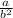`(a)/(b^(2) )` and the common ratio is
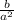`(b)/(a^(2) )`, so we get:

first term =
`(a)/(b^(2) )`

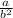
second term = first term * common ratio =
`(a)/(b^(2) ) *(b)/(a^(2) ) = (1)/(ab)`

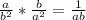
third term = second term * common ratio =
`(1)/(ab) *(b)/(a^(2) ) =(1)/(a^(3) )`

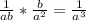
fourth term = third term * common ratio =
`(1)/(a^(3) ) *(b)/(a^(2) ) = (b)/(a^(5) )`

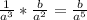
fifth term = fourth term * common ratio=
`(b)/(a^(5) ) *(b)/(a^(2) ) = (b^(2) )/(a^(7) )`

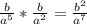
sixth term = fifth term * common ratio=
`(b^(2) )/(a^(7) ) *(b)/(a^(2) ) = (b^(3) )/(a^(9) )`

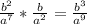
so, the next five terms are:

`(1)/(ab) , (1)/(a^(3) ) ,(b)/(a^(5) ) ,(b^(2) )/(a^(7) ) ,(b^(3) )/(a^(9) )`