In mathematics, the arrangement of numbers that have a definite pattern is a progression. There are three types of progression: arithmetic, harmonic and geometric. Arithmetic sequence have a common difference, harmonic sequence is the reciprocal of arithmetic sequence, and geometric sequence have a common ratio. For this problem, it is a geometric sequence.
8/2 = 4
32/8 = 4
128/32 = 4
512/128 = 4
The common ratio is 4. The equation for geometric sequence for the sum of terms is:
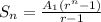
where n is the last term of the progression
A1 is the first term of the progression
r is the common ratio
Substituting the values,
 S12 = 11,184,810
S12 = 11,184,810