Question

Given the sequence: {2, 8, 32, 128, 512…}, S12 = ???

Answer 1

In mathematics, the arrangement of numbers that have a definite pattern is a progression. There are three types of progression: arithmetic, harmonic and geometric. Arithmetic sequence have a common difference, harmonic sequence is the reciprocal of arithmetic sequence, and geometric sequence have a common ratio. For this problem, it is a geometric sequence.

8/2 = 4
32/8 = 4
128/32 = 4
512/128 = 4

The common ratio is 4. The equation for geometric sequence for the sum of terms is:


`S_(n) = ( A_(1)( r^(n)-1) )/(r-1)`

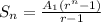
where n is the last term of the progression
A1 is the first term of the progression
r is the common ratio

Substituting the values,


`S_(12) = (2( 4^(12)-1) )/(4-1)`
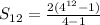S12 = 11,184,810