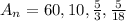
Using geometric sequence form, we can rewrite it as:
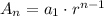
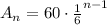
Since r < 1, there exists a limit, and thus, it is said to converge.
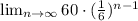
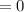
Since the ratio is still positive, as n tends towards infinity, the graph of the sequence will never go below the horizontal. Thus, we say that the limit of the function is zero, which means that as we increase the size of n, eventually after the infinite-th time, it will hit zero.