Since they are all unique letters, we don't need to worry about overcounting factors.
Now, we want
arrangements, so the order does matter. The arrangement: OLI is not the same as ILO, since they are counted as different words.
Thus, using the permutation formula, we get:
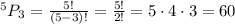
So, the answer is (A) 60