Answer:
A quadratic equation is in the form of
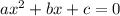 ........[1], then the solution for this equation is given by:
........[1], then the solution for this equation is given by:
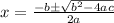
As per the statement:
The equation is given by:
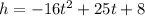
where, h is the height in feet t seconds after it is thrown.
After the ball passes its maximum height, it comes down and then goes into the hoop at a height of 10 feet above the ground.
⇒h = 10 feet
then;

Subtract 10 from both sides we have;

On comparing this equation with [1] we have;
a =16 , b =-25 and c =2
then;

⇒
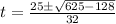
⇒

as we want the time when it was falling so ,
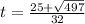
Simplify:
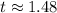 sec
sec
Therefore, 1.48 sec long after it was thrown does it go into the hoop