Question

Which complex number has a distance of √17 from the origin on the complex plane?

A;2 + 15i
B:17 + i
C:20 – 3i
D:4 – i

Answer 1

Let the complex number be x + iy

Then by the pythagoras therem

17 = x^2 + y^2

D will satisfy this equation

4^2 + (-1)^2 = 17

answer is D 4 - i

Answer 2

The complex number 4-i has distance
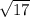`√(17)` from origin.

D is correct

Explanation:

We are given the absolute value of complex plane.

If complex number is a+ib then absolute value
`√(a^2+b^2)`

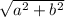
We have to check the absolute value of each option and check which is equal to
`√(17)`

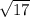
Option A: 2+15i

`d=√(2^2+15^2)=√(4+225)=√(229)\\eq √(17)`

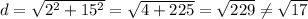
Option B: 17+i

`d=√(17^2+1^2)=√(289+1)=√(290)\\eq √(17)`

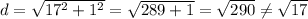
Option C: 20-3i

`d=√(20^2+3^2)=√(400+9)=√(409)\\eq √(17)`

Option D: 4-i

`d=√(4^2+1^2)=√(16+1)=√(17)= √(17)`

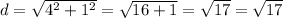
Hence, The complex number 4-i has distance
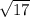`√(17)` from origin.