Question

For the function f(x) = –2(x + 3)2 − 1, identify the vertex, domain, and range. The vertex is (3, –1), the domain is all real numbers, and the range is y ≥ –1. The vertex is (3, –1), the domain is all real numbers, and the range is y ≤ –1. The vertex is (–3, –1), the domain is all real numbers, and the range is y ≤ –1. The vertex is (–3, –1), the domain is all real numbers, and the range is y ≥ –1.

Answer 1

we have

`f(x)=-2(x+3)^(2)-1`

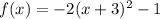
we know that

the equation of a vertical parabola in vertex form is equal to

`y=a(x-h)^(2)+k`

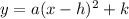
where

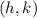`(h,k)` is the vertex

If
`a > 0` ------> then the parabola open upward (vertex is a minimum)

If
`a < 0` ------> then the parabola open downward (vertex is a maximum)

In this problem

the vertex is the point
`(-3,-1)`

`a=-2`

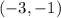
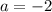
so

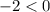`-2 < 0` ------> then the parabola open downward (vertex is a maximum)

The domain is the interval-------> (-∞,∞)

that means------> all real numbers

The range is the interval--------> (-∞, -1]

`y\leq-1`

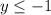
that means

all real numbers less than or equal to
`-1`

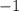
therefore

the answer is

a) the vertex is the point
`(-3,-1)`

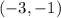
b) the domain is all real numbers

c) the range is
`y\leq-1`

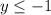
see the attached figure to better understand the problem