Question

An acute angle θ is in a right triangle with sin θ = two thirds . What is the value of cot θ?

Answer 1

six divided by the square root of thirteen

Explanation:

hey there,

< sin θ =
`(O)/(H)`

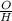
So that means O = 2 and H = 3. In order to find cot θ, first let's find tan θ.

tan θ =
`(O)/(B)`

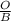
We only know what O is equal to, not B. So let's draw out a triangle.

7

◢ 6

B

As you can see (sorry for the poor triangle), this is a right triangle. In order to find an unknown part, use
`a^2 + b^2 = c^2`!

`6^2 + B^2 = 7^2`

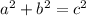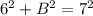
B = ±√13

Obviously, a side of a triangle can't be negative, so it stays positive. Now we can find tangent!

tanθ =
`(6)/(√(13) )`

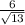
But, we're not done here. We're trying to find cotθ.

cotθ =
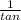`(1)/(tan)`θ

`(1)/((6)/(√(13) ) )` =
`(√(13) )/(6)`

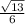
That's your final answer! >

Hope this helped! Feel free to ask anything else.

Answer 2

check the picture below.