Question

How does changing the function from f(x) = −5 cos 2x to g(x) = −5 cos 2x − 3 affect the range of the function?

Answer 1

[-8,2]

Explanation:

We are given that the function f(x) is transformed to the function g(x), where,

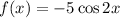`f(x) =-5 \cos 2x` and
`g(x) =-5 \cos 2x-3`.

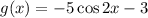Since, the range of
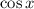`\cos x` is [-1,1].

Thus, the range of
`a\cos bx` is {-a,a].

So, the range of
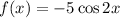`f(x) =-5 \cos 2x` is [-5,5].

As, we are translating the function f(x) 3 units downward to get g(x).

The graph of the function is shifted 3 units down.

So, the range of g(x) will be [-5-3,5-3] = [-8,2].

Hence, the range of
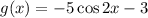`g(x) =-5 \cos 2x-3` is [-8,2].

Answer 2

The graph has been moved 3 units downward, making the range change. The range of f(x) is [-5,5], while the range of g(x) is [-8,2]. The picture is of both functions. f(x) is blue, g(x) is red.