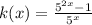Question

You have two exponential functions. One function has the formula g(x) = 5 x . The other function has the formula h(x) = 5-x . Which option below gives formula for k(x) = (g - h)(x)?

Answer 1

The value of
`k(x)=(5^(2x)-1)/(5^x)`

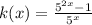
Explanation:

We have given two function
`g(x)=5^x\text{and}h(x)=5^(-x)`

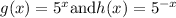
We have to find k(x)=(g-h)(x)

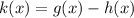`k(x)=g(x)-h(x)` (1)

We will substitute the values in equation (1) we will get

`k(x)=5^x-(5^(-x))`

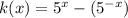
Now, open the parenthesis on right hand side of equation we will get

`k(x)=5^x-5^(-x)`

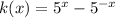
Using
`x^(-a)=(1)/(x^a)`

`k(x)=5^x-(1)/(5^x)`

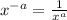
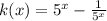
Now, taking LCM which is
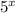`5^x` we will get after simplification

`k(x)=(5^(2x)-1)/(5^x)`

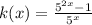
Hence, the value of
`k(x)=(5^(2x)-1)/(5^x)`

Answer 2

given the exponential functions
`g(x)= 5^(x)` and
`h(x)= 5^(-x)`


`k(x)=(g-h)(x)`

`k(x)=g(x)-h(x)`

`k(x)= 5^(x) - 5^(-x)`

`k(x)= 5^(x) - (1)/( 5^(x) )`

`k(x)= ( 5^(x) 5^(x) )/( 5^(x) ) - (1)/( 5^(x) )`

`k(x)= ( 5^(2x) )/( 5^(x) ) - (1)/( 5^(x) )`

`k(x)= ( 5^(2x)-1 )/( 5^(x) )`