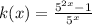Answer:
The value of
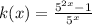
Explanation:
We have given two function

We have to find k(x)=(g-h)(x)
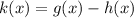 (1)
(1)
We will substitute the values in equation (1) we will get
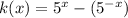
Now, open the parenthesis on right hand side of equation we will get
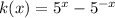
Using

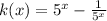
Now, taking LCM which is
 we will get after simplification
we will get after simplification
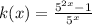
Hence, the value of