Given:
Required:
To find the value of x.
Step-by-step explanation:
The line that touches the circle is a tangent line.
We know that the line drawn from the centre of the circle to the tangent is perpendicular.
Thus the given triangle is the right angle triangle.
Where adjacent= 16
opposite = x
and hypotenuse = 8+x
Use the Pythagoras theorem:
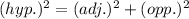
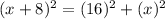
Use the identity:
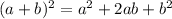
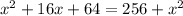
Solve by cancelling out the same term.
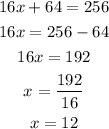
Final answer:
The value of x=12