Question

Solve for x. Assume that lines that which appears to be tangent are tangent. This is geometry(:

Answer 1

To solve for x, we need to find the equation of the tangent line at t = 25s. The slope of the tangent line is approximately 140.0.

Step-by-step explanation:

To solve for x, we need to find the equation of the tangent line at t = 25s. From the given information, we know that the endpoints of the tangent are (19, 1300) and (32, 3120). We can use the slope formula:



slope = (y2 - y1) / (x2 - x1)



Substituting the values:



slope = (3120 - 1300) / (32 - 19)


slope = 1820 / 13


slope ∼ 140.0

Answer 2

Given:

Required:

To find the value of x.

Step-by-step explanation:

The line that touches the circle is a tangent line.

We know that the line drawn from the centre of the circle to the tangent is perpendicular.

Thus the given triangle is the right angle triangle.

Where adjacent= 16

opposite = x

and hypotenuse = 8+x

Use the Pythagoras theorem:

`(hyp.)^2=(adj.)^2+(opp.)^2`
`(x+8)^2=(16)^2+(x)^2`

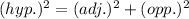
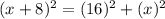
Use the identity:

`(a+b)^2=a^2+2ab+b^2`
`x^2+16x+64=256+x^2`

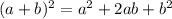
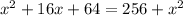
Solve by cancelling out the same term.

`\begin{gathered} 16x+64=256 \\ 16x=256-64 \\ 16x=192 \\ x=(192)/(16) \\ x=12 \end{gathered}`

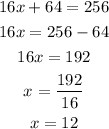
Final answer:

The value of x=12