Answer: 40.5 inches
Explanation:
Given: A city’s annual rainfall totals are normally distributed.
The probability that the city gets more than 43.2 inches of rain in a year is given by P(z≥1.5)=0.0668
Thus, X=43.2 inches
z=1.5
Standard deviation
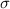 =1.8 inches
=1.8 inches
We know that
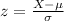

Hence, the city’s mean annual rainfall is 40.5 inches.