Question

If (x2 + x+ 1 ) is a factor of the polynomial 3x3 + 8x2 + 8x + 3 + 5k. find the value of k

Answer 1

One way to do this is apply the polynomial remainder theorem. First, note that


`x^2+x+1=\left(x+\frac12-\frac{\sqrt3}2i\right)\left(x+\frac12+\frac{\sqrt3}2i\right)`

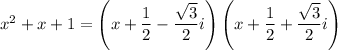
which means either of
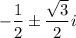
`-\frac12\pm\frac{\sqrt3}2i` are roots to
`3x^3+8x^2+8x+3+5k`.

The polynomial remainder theorem states that the remainder upon dividing a polynomial
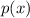
`p(x)` by a linear expression
`x-c` is equal to the value of
`p(c)`.

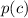
So what our factorization above tells us is that if we plug in, for example,
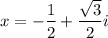
`x=-\frac12+\frac{\sqrt3}2i`, we would get


`3\left(-\frac12+\frac{\sqrt3}2i\right)^3+8\left(-\frac12+\frac{\sqrt3}2i\right)^2+8\left(-\frac12+\frac{\sqrt3}2i\right)+3+5k=0`

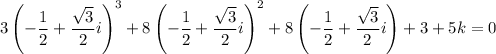
Expanding the left hand side gives


`-5+3+5k=0\implies5k=2\implies k=\frac25`

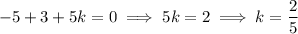
Alternatively, you could have determined the quotient and remainder via long division, which you would find to be


`(3x^3+8x^2+8x+3+5k)/(x^2+x+1)=\underbrace{3x+5}_\text{quotient}+\underbrace{(-2+5k)/(x^2+x+1)}_\text{remainder}`

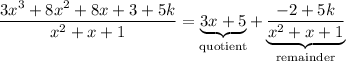
Then, since you know
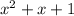
`x^2+x+1` is a factor of the cubic polynomial, you also know that the remainder should be 0, which means we're left with the equation


`-2+5k=0\implies5k=2\implies k=\frac25`

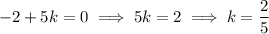
as expected.