Question

The function h(x) = x2 + 14x + 41 represents a parabola.

Part A: Rewrite the function in vertex form by completing the square. Show your work. (6 points)
Part B: Determine the vertex and indicate whether it is a maximum or a minimum on the graph. How do you know? (2 points)
Part C: Determine the axis of symmetry for h(x). (2 points)

Answer 1

to anyone who may be a lil' sus, the previous answer is correct.

Answer 2

Part A:


`h(x)= x^(2) +14x+41`

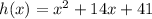
The first step of completing the square is writing the expression
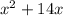
`x^(2) +14x` as
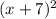
`(x+7)^(2)` which expands to
`x^(2) +14x+49`.

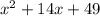
We have the first two terms exactly the same with the function we start with:
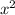
`x^(2)` and
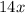
`14x` but we need to add/subtract from the last term, 49, to obtain 41.

So the second step is to subtract -8 from the expression
`x^(2) +14x+49`

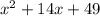
The function in completing the square form is

`h(x)= (x+7)^(2)-8`

Part B:

The vertex is obtained by equating the expression in the bracket from part A to zero


`x+7=0`

`x=-7`

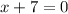
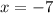
It means the curve has a turning point at x = -7

This vertex is a minimum since the function will make a U-shape.
A quadratic function
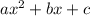
`a x^(2) +bx+c` can either make U-shape or ∩-shape depends on the value of the constant
`a` that goes with
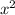
`x^(2)`. When
`a` is (+), the curve is U-shape. When
`a` (-), the curve is ∩-shape

Part C:

The symmetry line of the curve will pass through the vertex, hence the symmetry line is
`x=-7`

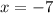
This function is shown in the diagram below