Answer:
The transformation of the function f(x) to g(x) is a horizontal stretch.
Explanation:
The parent function f(x) is given by:
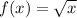
and the transformed function g(x) is given by:
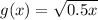
Now we know that the transformation of the type:
f(x) → f(bx)
is a horizontal stretch if 0<b<1
and is a horizontal shrink if b>1
Here we have:
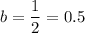
i.e.
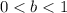
This means that the transformation of the function f(x) to g(x) is a horizontal stretch by a factor of 2.