Question

Describe the transformation of the graph of f into the graph of g as either a horizontal or vertical stretch. f(x)=sqrt(x) and g(x)=sqrt(0.5x)

Answer 1

`\bf \qquad \qquad \qquad \qquad \textit{function transformations} \\ \quad \\\\ % left side templates \begin{array}{llll} f(x)=&{{ A}}({{ B}}x+{{ C}})+{{ D}} \\ \quad \\ y=&{{ A}}({{ B}}x+{{ C}})+{{ D}} \\ \quad \\ f(x)=&{{ A}}\sqrt{{{ B}}x+{{ C}}}+{{ D}} \\ \quad \\ f(x)=&{{ A}}(\mathbb{R})^{{{ B}}x+{{ C}}}+{{ D}} \\ \quad \\ f(x)=&{{ A}} sin\left({{ B }}x+{{ C}} \right)+{{ D}} \end{array}\\\\ --------------------\\\\`


`\bf \bullet \textit{ stretches or shrinks horizontally by } {{ A}}\cdot {{ B}}\\\\ \bullet \textit{ flips it upside-down if }{{ A}}\textit{ is negative}\\ \left. \qquad \right. \textit{reflection over the x-axis} \\\\ \bullet \textit{ flips it sideways if }{{ B}}\textit{ is negative}\\ \left. \qquad \right. \textit{reflection over the y-axis}`


`\bf \bullet \textit{ horizontal shift by }\frac{{{ C}}}{{{ B}}}\\ \left. \qquad \right. if\ \frac{{{ C}}}{{{ B}}}\textit{ is negative, to the right}\\\\ \left. \qquad \right. if\ \frac{{{ C}}}{{{ B}}}\textit{ is positive, to the left}\\\\ \bullet \textit{ vertical shift by }{{ D}}\\ \left. \qquad \right. if\ {{ D}}\textit{ is negative, downwards}\\\\ \left. \qquad \right. if\ {{ D}}\textit{ is positive, upwards}\\\\ \bullet \textit{ period of }\frac{2\pi }{{{ B}}}`

with that template in mind, let's see
`\bf f(x)=√(x)\qquad \begin{array}{llll} g(x)=&√(0.5x)\\ &\quad \uparrow \\ &\quad B \end{array}`

so B went form 1 on f(x), down to 0.5 or 1/2 on g(x)
B = 1/2, thus the graph is stretched by twice as much.

Answer 2

The transformation of the function f(x) to g(x) is a horizontal stretch.

Explanation:

The parent function f(x) is given by:

`f(x)=√(x)`

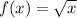
and the transformed function g(x) is given by:

`g(x)=√(0.5x)`

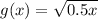
Now we know that the transformation of the type:

f(x) → f(bx)

is a horizontal stretch if 0<b<1

and is a horizontal shrink if b>1

Here we have:

`b=(1)/(2)=0.5`

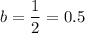
i.e.

`0<b<1`

This means that the transformation of the function f(x) to g(x) is a horizontal stretch by a factor of 2.