Answer: Solution is,
d. (2, 0)
Explanation:
Since, the equation of line that passes through points
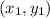 and
and
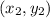 is,
is,
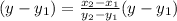
Thus, the equation of line through the points (3, 1) and (–5, –7) is,
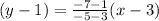
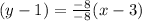

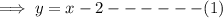 ,
,
Equation of second line is,
 ,
,
By equation (1) and (2),
x - 2 = 0.5x - 1 ⇒ 0.5x = 1 ⇒ x = 2,
From equation (1),
We get, y = 0,
Hence, the solution of line (1) and (2) is (2,0).