Which of the following correctly describes the end behavior of the polynomial function, f(x)=3x^4+2x^2-x

Question

asked Oct 24, 2018 74.6k views

2 Answers

Avimoondra · Answer 1 · 2018-10-29T22:10:17+0000

Answer:

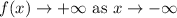
$f(x)\rightarrow +\infty\text{ as }x\rightarrow -\infty$

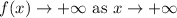
$f(x)\rightarrow +\infty\text{ as }x\rightarrow +\infty$

Explanation:

Given polynomial function is,

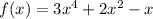
f(x)=3x^4+2x^2-x

Since, the end behavior of a polynomial is same as the end behavior of leading term,

Here, the leading term =
3x^4

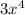
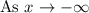
$\text{As }x\rightarrow -\infty$

The leading term is positive,

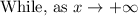
$\text{While, as }x\rightarrow +\infty$

The leading term is positive,

Hence, the end behavior of the given polynomial is,

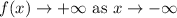
$f(x)\rightarrow +\infty\text{ as }x\rightarrow -\infty$

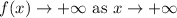
$f(x)\rightarrow +\infty\text{ as }x\rightarrow +\infty$

⇒ In the graph of f(x), both ends will go upward.