Answer:
Symmetry about y-axis
Explanation:
We are given that
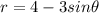
When the graph is symmetric about x- axis then the point (x,y) change in to (x,-y) and the function remain same.
The point
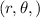 is replaced by
is replaced by
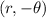
Substitute the value then we get

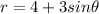 (
(
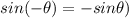
The value of function changes .Hence , the function is not symmetric about x- axis.
When the function is symmetric about y-axis then the point
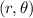 change into point
change into point
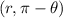 and function remain same
and function remain same
Substitute the value

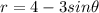 (
(
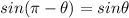 )
)
The value of function does not change when point change ,Hence, the function is symmetric about y- axis.
When the graph is symmetric about origin then the point
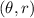 change into point
change into point
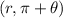 and the value of function remain same.
and the value of function remain same.
Substitute the value then we get
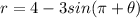
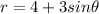
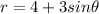
Hence, the graph has symmetry about y-axis .