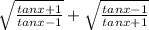Let's find at first
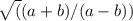
Let's find (a+b)(a-b)....
we should divide both side of fraction by b and we will get the following:
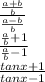
and (a-b)/(a+b) is same as (1/[(a+b)/(a-b)]) so we can use previous answer and finally we will have (a-b)/(a+b) = 1/[ (tanx + 1) / (tanx - 1)] = (tanx - 1)/(tanx + 1) and final answer will be this: