Answer:
The dimensions of the rectangle. Length= 15 inches and Width= 8 inches
Explanation:
Let width of rectangle be W and length be L then
L=W+7 ---- (A)
Also given that area of rectangle = 120 square inches
=> WxL=120 -----(B)
From equation (A) and (B)
Wx(W+7) = 120
=>
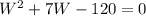
=>
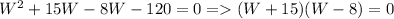
=>
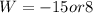
Since the width can not be a negative quantity , so W= 8 inches
=> L= W+7= (8+7) inches = 15 inches
Thus the dimensions of the rectangle. Length= 15 inches and Width= 8 inches