Answer:
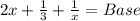
Explanation:
Given: The area of the parallelogram is
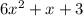 and the height is 3x.
and the height is 3x.
To find: The base of the given parallelogram.
Solution: It is given that The area of the parallelogram is
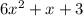 and the height is 3x.
and the height is 3x.
Now, area of parallelogram is given as:
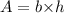 where b is the base and h is the height of teh gievn parallelogram.
where b is the base and h is the height of teh gievn parallelogram.
Substituting the given values, we have
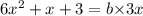
⇒
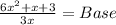
⇒

⇒
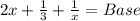
which is the required expression for the base of the given parallelogram.