Answer:
Joint variation says that:
if
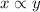 and
and
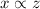
then the equation is in the form of:
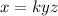 , where, k is the constant of variation.
, where, k is the constant of variation.
As per the statement:
If x varies jointly as y and z
then by definition we have;
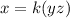 ......[1]
......[1]
Solve for k;
when x = 8 , y=4 and z=9
then
Substitute these in [1] we have;
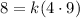
⇒
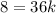
Divide both sides by 36 we have;

Simplify:
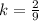
⇒
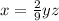
to find z when x = 16 and y = 6
Substitute these value we have;
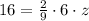
⇒
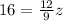
Multiply both sides by 9 we have;
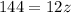
Divide both sides by 12 we have;
12 = z
or
z = 12
Therefore, the value of z is, 12