Question

A test consists of 20 problems and students are told to answer any 10 of these questions. In how many different ways can they choose the 10 questions?

Answer 1

We must find UNIQUE combinations because choosing a,b,c,d... is the same as d,c,b,a...etc. For this type of problem you use the "n choose k" formula...

n!/(k!(n-k)!), n=total number of choices available, k=number of choices made..

In this case:

20!/(10!(20-10)!)

20!/(10!*10!)

184756

Answer 2

Answer: The required number of ways is 184756.

Step-by-step explanation: Given that a test consists of 20 problems and students are told to answer any 10 of these questions.

We are to find the number of different ways in which the students choose 10 questions.

We know that

the number of ways in which r things can be chosen from n different things is given by

`N=^nC_r.`

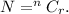
Therefore, the number of ways in which students chose 10 questions from 20 different questions is given by

`N\\\\=^(20)C_r\\\\\\=(20!)/(10!(20-10)!)\\\\\\=(20*19*18*17*16*15*14*13*12*11*10!)/(10!* 10*9*8*7*6*5*4*3*2*1)\\\\\\=184756.`

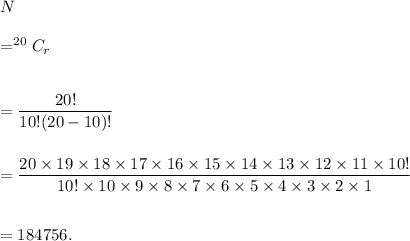
Thus, the required number of ways is 184756.