Question

What are the explicit equation and domain for an arithmetic sequence with a first term of 5 and a second term of 3?

Answer 1

1. 
   `a_n=7-2n`
2. All positive integers greater than 1 will be its domain.

Explanation:

The explicit equation for an arithmetic sequence is,

`a_n=a_1+(n-1)d`

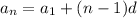
Where,

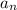`a_n` = nth term in the arithmetic sequence,

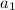`a_1` = 1st term in the arithmetic sequence,

d = common difference.

Here, the first term of 5 and a second term of 3. So the common difference is -2.

Putting the values,

`a_n=5+(n-1)(-2)=5+2-2n`

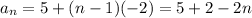
i.e
`a_n=7-2n`

As n neither be negative nor fraction, because it is the number of term, so all positive integers greater than 1 will be its domain.

Answer 2

Any arithmetic sequence can be expressed as:

a(n)=a+d(n-1), a=initial term, d=common difference, n=term number

In this case a=5, and d=-2 so

a(n)=5-2(n-1) which can be simplified...

a(n)=5-2n+2

a(n)=7-2n

The domain is restricted to integers from 1 to +oo.