Answer: The required value is P(A intersection B) = 0.20.
Step-by-step explanation: Given that for two independent events A and B,
P(A) = 0.40 and P(B) = 0.50.
We are to find the value of
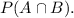
For any two independent events, the probability of their intersection is equal to the product of their probabilities.
Since A and B are independent events, so we have
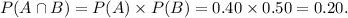
Thus, the required probability of the intersection of A and B is 0.20.
That is, P(A intersection B) = 0.20.