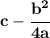Question

Please Help ASAP

A vehicle factory manufactures cars. The unit cost C (the cost in dollars to make each car) depends on the number of cars made. If x cars are made, then the unit cost is given by the function C(x) =x^2-320x+40,052 . What is the minimum unit cost? Do not round your answer.

Answer 1

the C(x) equation is a parabola with a squared "x" and a positive leading term coefficient, meaning, is a vertical parabola and it opens upwards

the lowest point, or lowest cost value, it reaches, is the U-turn point, or vertex


`\bf \textit{ vertex of a vertical parabola, using coefficients}\\\\ \begin{array}{llccll} y = &{{ 1}}x^2&{{ -320}}x&{{ +40052}}\\ &\uparrow &\uparrow &\uparrow \\ &a&b&c \end{array}\qquad \left(-\cfrac{{{ b}}}{2{{ a}}}\quad ,\quad {{ c}}-\cfrac{{{ b}}^2}{4{{ a}}}\right)`

so, the lowest cost is at
`\bf {{ c}}-\cfrac{{{ b}}^2}{4{{ a}}}`