Determine algebraically whether the function is even, odd, or neither even nor odd. f as a function of x is equal to 2 divided by x squared. Neither Even Odd

Question

asked Jul 5, 2018 28.8k views

2 Answers

ZJay · Answer 1 · 2018-07-09T18:41:51+0000

Answer:

Even

Explanation:

A function is said to be even function if we put -x instead of x and we get the same result of both function. i.e. f(-x) = f(x)

A function is said to be odd function if we put -x instead of x and we get the result as negative of that function. i.e. f(-x) = -f(x)

Now we have function, f(x) =
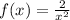
f(x) = (2)/(x^(2))

Now putting -x in place of x

$f(-x) = (2)/((-x)^(2))\\ = (2)/(x^(2)) = f(x)$

Hence, given function is an Even function.