Answer:
3 positive real root and 1 negative real root and no complex root.
Explanation:
Here, the given function,
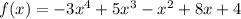
Since, the coefficient of variables are,
-3, 5, -1, 8, 4,
The sign of variables goes from Negative(-3) to positive (5) , positive(5) to negative(-1) and negative (-1) to positive (8),
So, the total changes in sign = 3,
By the Descartes's rule of sign,
Hence, the number of real positive roots = 3,
Also,
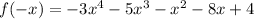
Since, the coefficient of variables are,
-3, -5, -1, -8, 4
The sign of varibles goes to negative (-8) to positive (4),
So, the total changes in sign = 1,
Hence, the number of real negative roots = 1,
Now, the degree of the function f(x) is 4,
Thus, the highest number of roots of f(x) is 4,
So, it does not have any complex root.