Step 1
Find the equation of the line that passes through points
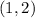 and
and
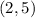
Find the slope of the line
The formula to calculate the slope is equal to
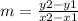
substitute the values
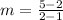
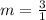
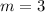
Find the equation of the line
The equation of the line into slope-point form is equal to
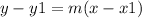
we have
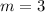
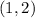
substitutes
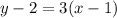
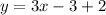
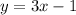
Step 2
Find the equation of the inequality
we know that
The solution is the shaded area below the solid line
therefore
the inequality is
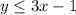
the answer is
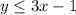
see the attached figure to better understand the problem