Answer:
The correct option is 4.
Explanation:
The given geometric sequence is
{1, -3, 9, ...}
Here the first term of the sequence is 1 and the common ratio is
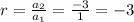
The explicit formula of a geometric sequence is
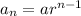
In the given geometric sequence a=1 and r=-3.
Substitute a=1 and r=-3 in the above formula.
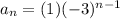
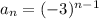
The explicit formula of given geometric sequence is
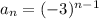 .
.
Therefore the correct option is 4.