Answer: the correct option is (B) 29.
Step-by-step explanation: We are given to find the length of the hypotenuse x, if (20, 21, x) is a Pythagorean triple.
We know that
in a right-angled triangle, the lengths of the sides (hypotenuse, perpendicular, base) is a Pythagorean triple, where
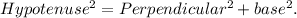
So, for the given Pythagorean triple, we have
![x^2=20^2+21^2\\\\\Rightarrow x^2=400+441\\\\\Rightarrow x^2=841\\\\\Rightarrow x=√(841)~~~~~~~~~~~~~~~~~[\textup{taking square root on both sides}]\\\\\Rightarrow x=\pm29.](https://img.qammunity.org/2018/formulas/mathematics/high-school/28p4id4fti65gvzppmc8tam36nqwwye944.png)
Since the length of the hypotenuse cannot be negative, so x = 29.
Thus, the length of the hypotenuse, x = 29.
Option (B) is CORRECT.