Answer: The initial values of the two functions are different but the rate of change is same.
Explanation:
For function A ,
When x=1, the initial value of function A=3
The rate of change of function A =
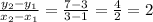
For function B,
When x=1, the initial value of function B= 4
The rate of change of function A =

Since, 3≠4, thus, the initial values of two function is different.
But the rate of change is same.
Thus, Function A has odd output values, because it has an odd number as initial value and 2 as constant rate of change.
Function B has even output values, because it has an even number as initial value and 2 as constant rate of change.