Question

Find the seventh term of the expansion of (4x-2y)^11

Answer 1

By the binomial theorem, which says


`(a+b)^n=\displaystyle\sum_(k=0)^n\binom nka^(n-k)b^k`

where
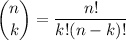
`\dbinom nk=(n!)/(k!(n-k)!)`, the seventh term of the expansion is given when
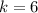
`k=6`. Take
`n=11`,
`a=4x`, and
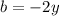
`b=-2y`, and we get


`\dbinom{11}6(4x)^(11-6)(-2y)^6=462\cdot4^5x^5\cdot(-2)^6y^6=7569408x^5y^6`

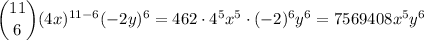
Note: it's possible that you may know the binomial theorem in the reverse direction, which says


`(a+b)^n=\displaystyle\sum_(k=0)^n\dbinom nka^kb^(n-k)`

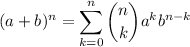
in which case the answer would be
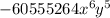
`-60555264 x^6 y^5`.

Answer 2

Answer: B on edg

Explanation: