Answer:
The length is 22 cm and the width is 6 cm
Explanation:
Let:
- l = length of the length of the rectangle (cm)
- w = length of the width of the rectangle (cm)
Equations:

Solve Using Substitution:
We know that l is 3w + 4. So input 3w + 4 for l in the top equation.
- 2( l + w ) = 56
- 2( 3w + 4 + w ) = 56
- 2( 4w + 4) = 56
- 8w + 8 = 56
- 8w = 48
- w = 6
Plugin New Info:
Now that we solved for w, we can solve for l by inputting the value of w in the second equation
- l = 3(6) + 4
- l = 18 + 4
- l = 22
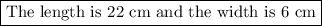
-Chetan K