Question

What is the coefficient of the fifth term in a binomial that is raised to the sixth power?

A.) 5
B.) 6
C.) 15
D.) 20

Answer 1

5 is your answer

Explanation:

Answer 2

C) 15

Explanation:

To find the coefficient of terms in a binomial expression, we can use the Pascal's triangle.

1

1 1

1 2 1

1 3 3 1

1 4 6 4 1

1 5 10 10 5 1

1 6 15 20 15 6 1

The binomial expression (x+y)^0, when power is zero, the answer is 1.

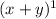`(x+y)^(1)` , when the power is 1, there two coefficients 1 and 1

When the power is 3, the number of coefficients 3, that is the coefficient of the first term is 1, the second term's coefficient is 2 and third term coefficient is 1.

Similarly, when the binomial expression raised to the sixth power, there will be 7 coefficients.

You can see it in the Pascal's triangle.

The coefficients are 1, 6, 15,20,15,6,1

We are asked to find the fifth term's coefficient.

It is 15.

Therefore, the coefficient's of the fifth term of binomial expression raised to the power six is 15.