Answer:
Robyn and Vladimir both are correct.
Explanation:
Vladimir says that the equation of the line the passes through points (-5, -3) and (10,9) is y =
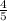 x + 1
x + 1
Let's find the equation of line
Slope of the line passing through ( -5, -3 ) and (10, 9 )
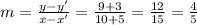
So equation will be y =
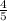 x + c
x + c
Since the line passes through (-5, -3)
so (-3) =
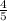 x (-5) + c
x (-5) + c
(-3) = -4 + c
c = -3 +4 = 1
So equation should be y =
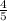 x +1
x +1
Therefore, Vladimir is correct.
Robyn says this line is passing through (-10,-7) and (-15, -11)
Slope

equation is y =
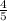 x + c
x + c
Since this line passes through (-10 -7)
so (-7) =
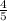 x (-10) + c
x (-10) + c
-7 = -8 + c ⇒ c = 8 - 7 = 1
Equation of the line will be y =
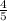 x + 1
x + 1
So Robyn and Vladimir both are correct.