Question

Vladimir says that the equation of the line that passes through points (-5,-3) and (10,9) is y=4/5x+1 Robyn says that the line passes through the points (-10,-7) and (-15,-11) Who is correct?

Answer 1

Both of them are correct

Explanation:

Given the equation: y = (4/5)*x + 1, we want to check if some points belongs to it. To do so, just replace the coordinates of the point in the equation and check if the equality is satisfied.

Point (-5, -3)

-3 = (4/5)*(-5) + 1

-3 = -3 -> equation satisfied

Point (10, 9)

9 = (4/5)*10 + 1

9 = 9 -> equation satisfied

Then, Vladimir is correct

Point (-10, -7)

-7 = (4/5)*(-10) + 1

-7 = -7 -> equation satisfied

Point (-15, -11)

-11 = (4/5)*(-15) + 1

-11 = -11 -> equation satisfied

Then, Robyn is correct.

Answer 2

Robyn and Vladimir both are correct.

Explanation:

Vladimir says that the equation of the line the passes through points (-5, -3) and (10,9) is y =
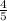`(4)/(5)` x + 1

Let's find the equation of line

Slope of the line passing through ( -5, -3 ) and (10, 9 )

`m=(y-y')/(x-x')=(9+3)/(10+5)=(12)/(15)=(4)/(5)`

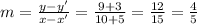
So equation will be y =
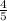`(4)/(5)`x + c

Since the line passes through (-5, -3)

so (-3) =
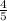`(4)/(5)`x (-5) + c

(-3) = -4 + c

c = -3 +4 = 1

So equation should be y =
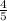`(4)/(5)`x +1

Therefore, Vladimir is correct.

Robyn says this line is passing through (-10,-7) and (-15, -11)

Slope
`m=(y-y')/(x-x')=(-11+7)/(15+10)=(-4)/(-5)=(4)/(5)`

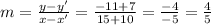
equation is y =
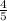`(4)/(5)`x + c

Since this line passes through (-10 -7)

so (-7) =
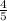`(4)/(5)`x (-10) + c

-7 = -8 + c ⇒ c = 8 - 7 = 1

Equation of the line will be y =
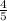`(4)/(5)`x + 1

So Robyn and Vladimir both are correct.