Expand (x - 4)^2:
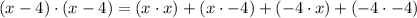
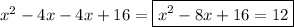
Subtract 12 from both sides to get one side to equal 0:
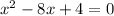
Find the values of a, b, and c in this quadratic equation:
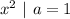
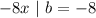
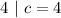
The quadratic formula is expressed as follows:
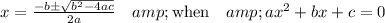
Plug in our values into the formula:
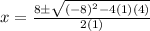
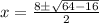
Simplify the square root:
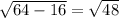
Prime factorize the square root:
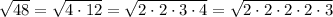
Take any number that is repeated twice in the square root, and move it outside:
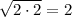
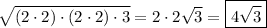
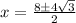
Solve the plus and minus:
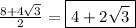
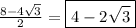
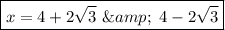
The answer is {4 + 2√3, 4 - 2√3}.