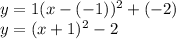Complete the statements below that show y = x2 + 2x - 1 being converted to vertex form

Question

asked Jan 21, 2018 87.5k views

2 Answers

KulaGGin · Answer 1 · 2018-01-25T20:31:54+0000

Answer:

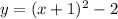
y=(x+1)^2-2

Explanation:

General polynomial formula of a quadratic equation

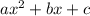
ax^2+bx+c

Equation
y= x^2+2x-1

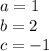
$a= 1\\ b=2\\ c=-1$

The formula to find the x coordinate of the vertex is

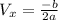
V_(x)= (-b)/(2a)

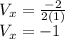
$V_(x)=(-2)/(2(1)) \\ V_(x)= -1$

Now to find the y coordinate of the vertex we substitute the found value of the x coordinate in
y= x^2+2x-1

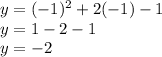
$y= (-1)^2+2(-1)-1 \\ y= 1-2-1\\ y=-2$

The general vertex formula for any quadratic function is

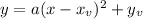
y= a(x-x_(v))^2+y_(v)

Replace

$y= 1(x-(-1))^2+(-2)\\ y=(x+1)^2-2$