Answer:
Angular velocity=0.785rad/s
Explanation:
Let us first consider the circumference of pendulum that is:
Circumference=
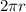 , where r is the radius.
, where r is the radius.
Now, it is given that the radius is= 6 foot , therefore
Circumference=

Circumference=

Now, Calculate enough time to produce a whole circular, by causing a proportion with both ratios:
Ratio 1 =
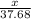 and Ratio 2=
and Ratio 2=
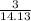
Thus, ratio 1 = ratio 2


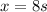
Also, Calculate the angular speed as the
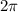 radian (which is the full total angle of the group) divided by enough time.
radian (which is the full total angle of the group) divided by enough time.
So the angular speed is =
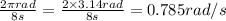 .
.