Question

The height of an arrow shot upward can be given by the formula s = v0t - 16t2, where v0 is the initial velocity and t is time. How long does it take for the arrow to reach a height of 48 ft if it has an initial velocity of 96 ft/s? Round to the nearest hundredth. The equation that represents the problem is 48 = 96t - 16t2. Solve 16t2 - 96t + 48 = 0. Complete the square to write 16t² - 96t + 48 = 0 as . Solve (t - 3)² = 6. The arrow is at a height of 48 ft after approximately s and after s.

Answer 1

(t-3)^2=6

Explanation:

Answer 2

The arrow is at a height of 48 ft after approximately 0.55 seconds and after 5.45 seconds.

Explanation

The given formula is:
`s=V_(0)t-16t^2`

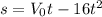
If the initial velocity is 96 ft/s , that means
`V_(0)=96`

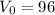
For finding the time the arrow takes to reach a height of 48 ft, we will plug
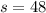`s= 48` into the above formula. So......

`48=96t-16t^2\\ \\ 16t^2-96t+48=0\\ \\ 16(t^2-6t+3)=0\\ \\ t^2-6t+3=0\\ \\ t^2-6t =-3\\ \\ t^2-6t+9=-3+9\\ \\ (t-3)^2 = 6\\ \\ t-3= \pm √(6) \\ \\ t=3\pm √(6)\\ \\ t = 5.45 , 0.55`

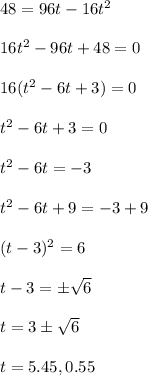
So, the arrow is at a height of 48 ft after approximately 0.55 seconds and after 5.45 seconds.