Question

Identify the quadratic function(s). (Select all that apply.) 8 - 5x = 4(3x - 1) (4a + 2)(2a - 1) + 1 = 0 2y + 2(3y - 5) = 0 2b(b - 7) + b = 0

Answer 1

A function is described as a quadratic function if the highest power of the variables of the function is 2.

For

`8 - 5x = 4(3x - 1)=12x-4 \\ \\ 12x+5x-8-4=0 \\ \\ 17x-12=0`
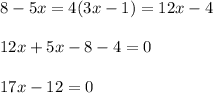
The highest power of x is 1, hence, the function is not a quadratic function.

For

`(4a + 2)(2a - 1) + 1 = 0 \\ \\ 8a^2-4a+4a-2+1=0 \\ \\ 8a^2-1=0`
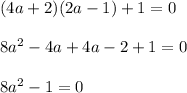
The highest power of a is 2, hence, the function is a quadratic function.

For

`2y + 2(3y - 5) = 0 \\ \\ 2y+6y-10=0 \\ \\ 8y-10=0`
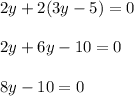
The highest power of y is 1, hence, the function is not a quadratic function.

For

`2b(b - 7) + b = 0 \\ \\ 2b^2-14b+b=0 \\ \\ 2b^2-13b=0`
The highest power of b is 2, hence, the function is a quadratic function.

Therefore, the quadratic functions are (4a + 2)(2a - 1) + 1 = 0 and 2b(b - 7) + b = 0