Answer:
Width of the sidewalk is 1.04 m
Explanation:
A rectangular garden plot has a central planting area with dimensions 13m by 8m.
There is a sidewalk around the parameter with a width of w.
So the dimensions of the total area will be (13 + 2w)m by (8 + 2w)m.
Planting area plus sidewalk area is given as 152 m²
Now the total area = Length × width
152 = (13 + 2w) × (8 + 2w)
152 = 8(13 + 2w) + 2w(13 + 2w) [Distributive law]
152 = 104 + 16w + 26w + 4w²
152 = 4w² + 42w + 104
4w² + 42w + 104 - 152 = 0
4w² + 42w - 48 = 0
2w² + 21w - 24 = 0
w =
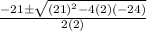
=
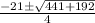
=
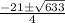
=
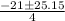
= 1.04 meters
Therefore, width of the sidewalk is 1.04 m